Have you ever wondered: What is a computer? What is computing? How do computers work? If these questions intrigue you, this article will take you through the fascinating origins of computer science, focusing on the Turing Machine.

The journey begins with a fundamental question: What is mathematics? Over time, many definitions emerged. Benjamin Peirce (1870) described it as logical reasoning: “Mathematics is the science that draws necessary conclusions.” Similarly, Bertrand Russell (1903) stated: “All mathematics is symbolic logic.”

Others leaned on intuitionism, viewing mathematics as the mental construction of ideas. However, David Hilbert introduced a revolutionary concept: mathematics as a formal system. A formal system uses an alphabet or meaningless symbols manipulated according to explicit rules, like chess pieces following their game rules.

Hilbert outlined three foundations for mathematics:

• Consistency: No contradictions exist (e.g., 1 = 2 is never true).
• Completeness: All true mathematical statements are provable.
• Decidability: A definitive procedure exists to determine the truth or falsity of a mathematical statement.

Hilbert’s concept of decidability required defining an “effective procedure.” Alan Turing, in the 1930s, developed a theoretical framework to address this. Inspired by human “computers” who solved problems by following step-by-step instructions, Turing envisioned a machine capable of performing any computation—the Turing Machine.

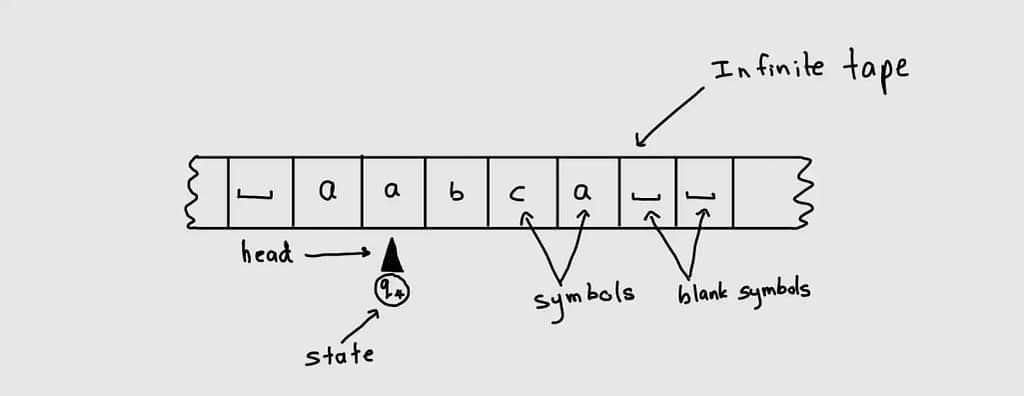
A Turing Machine is a simple yet powerful concept. It consists of:

• An infinite tape divided into squares, each holding a symbol or blank.
• A head that reads/writes symbols and moves left or right.
• A set of states, determining the machine’s actions based on the current state and symbol.
• Instructions defining how to process symbols and transition between states.

A Turing Machine is formally defined as a 7-tuple M=⟨Q,Γ,b,Σ,δ,q0,F⟩ where:

• Γ: A finite set of tape alphabet symbols.
• b∈Γ: The blank symbol (can appear infinitely).
• Σ⊆Γ: The set of input symbols allowed in the initial tape.
• Q: A finite set of states.
• q0∈Q: The initial state.
• F⊆Q: The set of final/accepting states.
• δ: The transition function, mapping state-symbol pairs to new state-symbol-direction triples.

The machine halts when δ is undefined for the current state and symbol.

Imagine a task: recognizing the sequence 000111 (equal numbers of zeros followed by ones). Here’s how a Turing Machine might solve it:

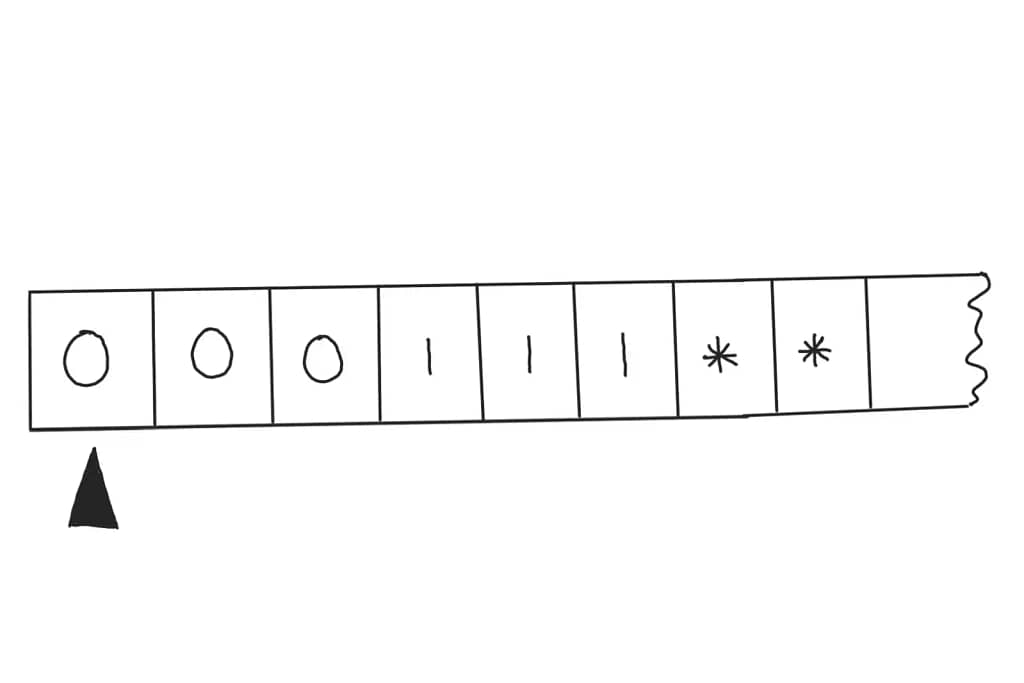
1. Replace the leftmost 0 with x and move right to find the first 1.
2. Replace the 1 with y and return left to the next 0.
3. Repeat until all 0s are x and all 1s are y.
4. Confirm no remaining 0s or 1s.

Example Walkthrough:

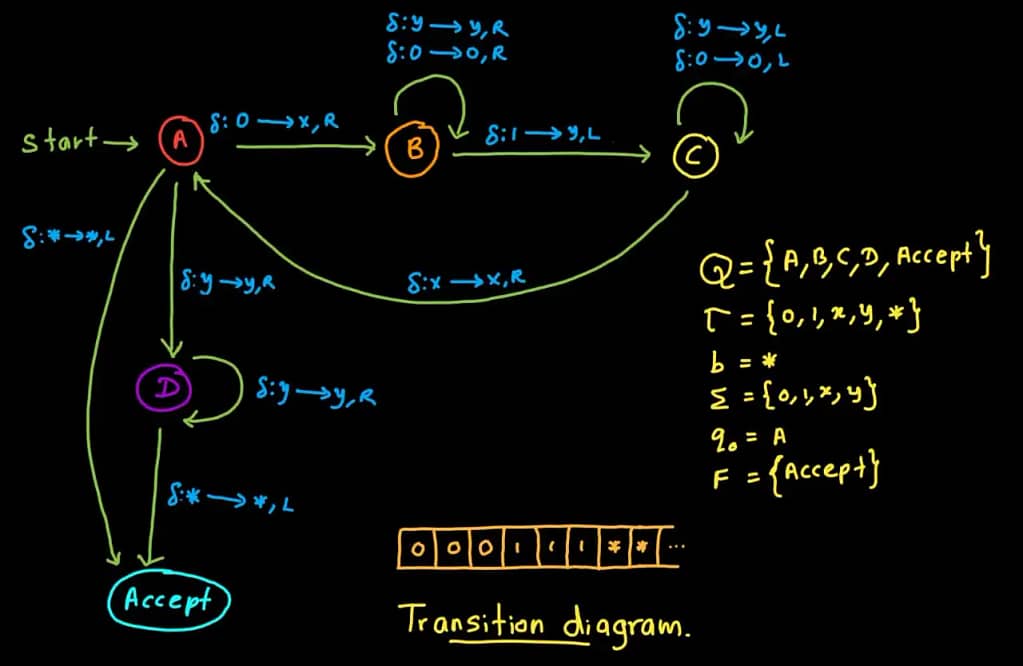
• Step 1: The machine starts in State A, reads the first 0, replaces it with x, and moves right to State B.
• Step 2: It skips over x and 0 symbols until it encounters the first 1. It replaces this 1 with y and transitions to State C, moving left.
• Step 3: The machine continues left until it finds the next x, transitioning back to State A.
• Step 4: Steps 1-3 repeat until all 0s and 1s are replaced.
• Step 5: If no more 0s or 1s remain and the head finds blanks, the machine halts in an ACCEPT state.

Turing later realized the instructions for different tasks could be encoded in binary (1s and 0s), enabling a single machine to execute any computation. This concept birthed the idea of programmable computers.

The Turing Machine revolutionized our understanding of computation. It demonstrated that any computational task can, in theory, be performed by such a machine. Alan Turing’s work laid the foundation for modern computing, influencing everything from algorithms to artificial intelligence.

If you are curious about Alan Turing, then this movie is for you.